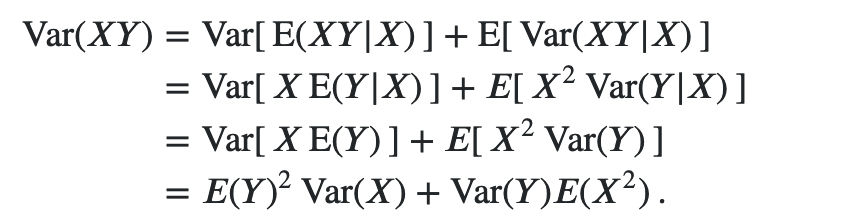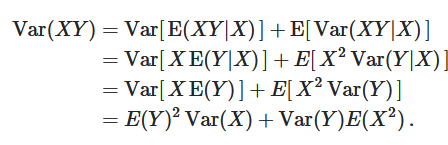“Statistics is not perfect, but it is beautiful and exquisite! ”
Theoretical Derivation This post is heavily focused on the mathematical proof and theoretical derivation, which doesn’t be discussed much in the “Statistics” Post.
Will be an appendix of it.
Gaussian Distribution Normally, we have Gaussian Distribution: X ∼ N ( μ , σ 2 ) .
We can now have ( X − μ ) ∼ N ( 0 , σ 2 ) , which is symmetric odd-function.
As for the properties of PDF and CDF , we have:
∫ − ∞ ∞ 1 2 π σ e − ( x − μ ) 2 2 σ 2 d x = 1 ∫ − ∞ ∞ x − μ 2 π σ e − ( x − μ ) 2 2 σ 2 d x = 0 Gaussian Probability Tables and Quantiles
Means of Gaussians For E [ x ] = μ ,
E ( x ) = ∫ − ∞ + ∞ x f ( x ) d x = ∫ − ∞ + ∞ x 2 π δ e − ( x − μ ) 2 2 δ 2 d x = ∫ − ∞ + ∞ ( x − μ ) + μ 2 π δ e − ( x − μ ) 2 2 δ 2 d x = ∫ − ∞ + ∞ x − μ 2 π δ e − ( x − μ ) 2 2 δ 2 d x ⏟ 0 + μ ∫ − ∞ + ∞ 1 2 π δ e − ( x − μ ) 2 2 δ 2 d x ⏟ 1 = μ
For E [ x 2 ] = σ 2 + μ 2 ,
E ( x 2 ) = ∫ − ∞ ∞ x 2 ⋅ 1 2 π σ e − ( x − μ ) 2 2 σ 2 d x = ∫ − ∞ ∞ ( x + μ ) ( x − μ ) + μ 2 2 π σ e − ( x − μ ) 2 2 σ 2 d x = ∫ − ∞ ∞ ( x + μ ) ( x − μ ) 2 π σ e − ( x − μ ) 2 2 σ 2 d x + ∫ − ∞ ∞ μ 2 2 π σ e − ( x − μ ) 2 2 σ 2 d x = ∫ − ∞ ∞ − σ ( x + μ ) 2 π d ( e − ( x − μ ) 2 2 σ 2 ) + μ 2 = ( − σ ( x + μ ) 2 π e − ( x − μ ) 2 2 σ 2 ) ∞ ⏟ 0 + σ 2 ∫ − ∞ ∞ 1 σ 2 π e − ( x − μ ) 2 2 σ 2 d x + μ 2 = σ 2 + μ 2
For E [ x 3 ] = 3 μ σ 2 + μ 3 ,
Patch up x 3 into ( x − μ ) 3 ,
So we have, substitutes with E [ x 2 ] and E [ x ] formulas:
E ( x 3 ) = ∫ − ∞ ∞ x 3 ⋅ 1 2 π σ e − ( x − μ ) 2 2 σ 2 d x = ∫ − ∞ ∞ ( x − μ ) 3 + μ 3 + 3 μ x 2 − 3 x μ 2 2 π σ e − ( x − μ ) 2 2 σ 2 d x = ∫ − ∞ ∞ ( x − μ ) 3 2 π σ e − ( x − μ ) 2 2 σ 2 d x ⏟ 0 + ∫ − ∞ ∞ 3 ( μ x 2 − x μ 2 ) 2 π σ e − ( x − μ ) 2 2 σ 2 d x + μ 3 = 0 + 3 ( μ E ( x 2 ) − μ 2 E ( x ) ) + μ 3 = 3 μ σ 2 + μ 3 For E [ x 4 ] = 3 σ 4 + 6 μ 2 σ 2 + μ 4 ,
Patch up x 4 ,
So we have,
E ( x 4 ) = ∫ − ∞ ∞ x 4 ⋅ 1 2 π σ e − ( x − μ ) 2 2 σ 2 d x = ∫ − ∞ ∞ ( x 2 + μ 2 ) ( x + μ ) ( x − μ ) 2 π σ e − ( x − μ ) 2 2 σ 2 d x + μ 4 = ∫ − ∞ ∞ ( x 2 + μ 2 ) ( x + μ ) 2 2 π σ e − ( x − μ ) 2 2 σ 2 d ( x − μ ) 2 + μ 4 = − ∫ − ∞ ∞ σ ( x 2 + μ 2 ) ( x + μ ) 2 π d e − ( x − μ ) 2 2 σ 2 + μ 4 = ( − σ ( x 2 + μ 2 ) ( x + μ ) 2 π e − ( x − μ ) 2 2 σ 2 ) ∞ ⏟ 0 + ∫ − ∞ ∞ e − ( x − μ ) 2 2 σ 2 d ( x 2 + μ 2 ) ( x + μ ) 2 2 π σ + μ 4 = 0 + σ 2 ( 3 ∗ E ( x 2 ) + 2 μ E ( x ) + μ 2 ) + μ 4 = 3 σ 4 + 6 μ 2 σ 2 + μ 4 For E [ X ¯ n ] = E [ X 1 ] ,
E [ X ¯ n ] = 1 n ∑ i = 1 n E [ X i ] = E [ X 1 ]
For E [ X Y ] ,
The expectation of the product of X and Y is the product of the individual expectations: E(XY ) = E(X)E(Y ) .
Variance of Gaussians For V [ x ] = σ 2 ,
With integral formulas step by step, we can get:
V = ∫ − ∞ + ∞ 1 2 π δ e − ( x − u ) 2 2 δ 2 ( x − u ) 2 d x = ∫ − ∞ + ∞ 1 2 π δ e − x 2 2 δ 2 x 2 d x = − δ 2 π ∫ − ∞ + ∞ x d ( e − x 2 2 δ 2 ) = − δ 2 π ( x e − x 2 2 δ 2 | − ∞ + ∞ ⏟ − ∫ − ∞ + ∞ e − x 2 2 δ 2 d x ) = δ 2 π ∫ − ∞ + ∞ e − x 2 2 δ 2 d x = δ 2
Which can be simplified with expectation substitutions we concluded above:
V ( x ) = E ( ( x − E ( x ) ) 2 ) = E ( x 2 − 2 x E ( x ) + E 2 ( x ) ) = E ( x 2 ) − 2 E ( x ) E ( x ) + E 2 ( x ) = E ( x 2 ) − E 2 ( x ) = E ( x 2 ) − μ 2 = σ 2
For V [ x 2 ] = 2 σ 4 + 4 σ 2 μ 2 ,
V ( x 2 ) = E ( x 4 ) − E ( x 2 ) 2 = 3 σ 4 + 6 μ 2 σ 2 + μ 4 − ( σ 2 + μ 2 ) 2 = 2 σ 4 + 4 σ 2 μ 2 4
V ( X ¯ n ) = σ 2 n
Var(XY)
Covariance Normally, we have standard covariance formula between variable x and y ,
Cov ( x , y ) = E [ ( x − E [ x ] ) ( y − E [ y ] ) ]
pdf
You should have something like:
E ( | X − Y | a ) = ∬ x > y ( x − y ) a d x d y + ∬ y > x ( y − x ) a d x d y = 2 ∬ x > y ( x − y ) a d x d y Now:
∬ x > y ( x − y ) a d x d y = ∫ y = 0 1 ∫ x = y 1 ( x − y ) a d x d y = 1 ( a + 1 ) ( a + 2 ) So:
E ( | X − Y | a ) = 2 ∬ x > y ( x − y ) a d x d y = 2 ( a + 1 ) ( a + 2 ) Covariance of Gaussians Recall that the covariance of two random variables X and Y denoted by Cov ( X , Y ) is defined as:
Cov ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] Cov ( X , Y ) = E [ X Y ] ⋅ E [ X ] E [ Y ] ) ] Var[X+Y] = Var[X] + Var[Y] + 2∙Cov[X,Y]
Var ( X Y ) = Var [ E ( X Y ∣ X ) ] + E [ Var ( X Y ∣ X ) ] = Var [ X E ( Y ∣ X ) ] + E [ X 2 Var ( Y ∣ X ) ] = Var [ X E ( Y ) ] + E [ X 2 Var ( Y ) ] = E ( Y ) 2 Var ( X ) + Var ( Y ) E ( X 2 ) If the covariance between two random variables is 0, then they are independent?
False, the criterion for independence is F ( x , y ) = F X ( x ) F Y ( y )
variance of ln function
Var[X] is known, how to calculate Var[ 1 x ]:
Using Delta Method,
You can use Taylor series to get an approximation of the low order moments of a transformed random variable. If the distribution is fairly 'tight' around the mean (in a particular sense), the approximation can be pretty good.
g ( X ) = g ( μ ) + ( X − μ ) g ′ ( μ ) + ( X − μ ) 22 g ′ ′ ( μ ) + … SO
Var [ g ( X ) ] = Var [ g ( μ ) + ( X − μ ) g ′ ( μ ) + ( X − μ ) 2 2 g ′ ′ ( μ ) + … ] = Var [ ( X − μ ) g ′ ( μ ) + ( X − μ ) 2 2 g ′ ′ ( μ ) + … ] = g ′ ( μ ) 2 Var [ ( X − μ ) ] + 2 g ′ ( μ ) Cov [ ( X − μ ) , ( X − μ ) 2 2 g ′ ′ ( μ ) + … ] + Var [ ( X − μ ) 2 2 g ′ ′ ( μ ) + … ] often only the first term is taken
In this case (assuming I didn't make a mistake), with g ( X ) = 1 X , Var [ 1 X ] ≈ 1 μ 4 Var ( X ) .
The Property of Maximum Given the IID r.v. X ∼ Uni ( 0 , 1 ) , we have M n = max ( x 1 , ⋯ , x n ) ,
Then, because X n are i.i.d. :
P ( M n < t ) = P ( ∩ i = 1 n { x i ≤ t } ) = ∏ i = q n P ( x i ≤ t ) ⟶ F X ( t ) n where F X ( ⋅ ) is the CDF of distribution.
P ( n ( 1 − M n ) ≤ t ) = P ( 1 − M n ≤ t n ) = P ( M n ≥ 1 − t n ) = 1 − P ( M n < 1 − t n ) = 1 − ( 1 − t n ) n ⟶ n → ∞ 1 − e − t . Limitations for anyconstant c :
Food for thought:
What is the variance of the maximum of a sample?
M n
b = - (2*barX_n + 1.6448^2/n)
(2 barX_n + 1.6448^2/n + sqrt((2 barX_n + 1.6448^2/n) &2-4*barX_n^2) )/2
Mode of Convergence Examples Example of a.s.
Let U ∼ Uni ( 0 , 1 ) , X n = U + U n (raised to the power of n )
Claim: X n ⟶ a.s U
Proof:
With law of total probability, for any event A ,
P ( A ) = P ( A ∣ S 1 ) P ( S 1 ) + P ( A ∣ S 2 ) P ( S 2 ) { X n ⟶ n → ∞ U if U ∈ ( 0 , 1 ) X n ⟶ n → ∞ 2 if U = 1 So we have
P ( X n ⟶ n → ∞ U ) = P ( X n ⟶ U ) P ( U < 1 ) + 0 = 1 Example 1 of P ,
Let X n ∼ i i d B e r ( 1 n ) and ϵ ∈ ( 0 , 1 ) , we have
Example 2 of P ,
Let U ∼ Uni ( 0 , 1 ) , X i = min X i
Claim: X ( 1 ) → p O ,
Proof:
Fix ε > 0 ,
P ( | X ( 1 ) − 0 | > ε ) = P ( X ( 1 ) > ε ) = P ( X i > ε , ∀ i ) = ( P ( X 1 > ε ) ) n = ( S ε 1 ∣ d x ) n = ( 1 − ε ) n → n → ∞ 0 Example of complying P but not with a.s.
Let U ∼ Uni ( 0 , 1 ) , x is more and more subdivided segmentation functions between [0, 1]:
𝟙 𝟙 𝟙 𝟙 𝟙 𝟙 x 1 = U + 1 ( U ∈ [ 0 , 1 ] ) = U + 1 x 2 = U + 1 ( U ∈ [ 0 , 1 / 2 ] ) x 3 = U + 1 ( U ∈ [ 1 / 2 , 1 ] ) x 4 = U + 1 ( U ∈ [ 0 , 1 / 3 ] ) x 5 = U + 1 ( U ∈ [ 1 / 3 , 2 / 3 ] ) x 6 = U + 1 ( U ∈ [ 2 / 3 , 1 ] ) Claim 1: x n → p U : Fix 0 < ε < 1
P ( | x n − U | > ε ) = P ( U ∈ [ a n , b n ] ) = b n − a n → n → ∞ 0 Claim 2: x n → a.s. U :
P ( x n → x ) ≠ 1 , x n has not limis Quadratic equation
![[eq2]](https://www.statlect.com/images/mean-estimation__10.png)
![[eq3]](https://www.statlect.com/images/mean-estimation__14.png)