“They are common in many areas and quite important to solve problem.”
Eigenvalues and Eigenvectors of a matrix
In this section, we will work with the entire set of complex numbers, denoted by
To illustrate the idea behind what will be discussed, consider the following example.
Compute
What do you notice about
Notice that for each,
When
Definition 7.1.1: Eigenvalues and Eigenvectors
Let A be an n×n matrix and let X∈Cn
be a nonzero vector for which
for some scalar λ. Then λ is called an eigenvalue of the matrix A and X is called an eigenvector of A associated with λ, or a λ-eigenvector of A.
The set of all eigenvalues of an n×n
matrix A is denoted by σ(A) and is referred to as the spectrum of A.
Haven’t Handled
Matrix
Understand the concept of eigenvalues and eigenvectors of an matrix.
inner product (also called the dot product )



row rank , column rank and normal rank

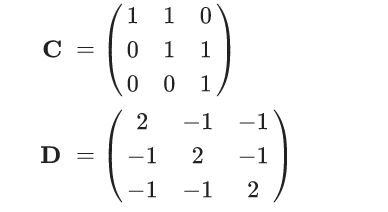

Geometric Interpretation of Eigenvalues and Eigenvectors
Determinant and Eigenvalues
Trace and Eigenvalues