“Machine Learning, Deep Learning, Data Science, etc. are all in the same nexus – which is the bacically Probability plus Statistics. ”

Statistics, MIT 18.6501x

A useful book and a probability refer link.

Where will be covered:

• Theorems and Tools

  • LLN & CLT, CMT

  • Hoeffding's Inequality, Chebyshev Inequality

  • Slutsky's theorem

  • Asymptotic normality

  • Delta ($\mathrm{\Delta }$$\Delta$) method

• Distribution Functions

• Mode of Convergence

• Estimator

• Probability Redux

   

Theorems and Tools

i.i.d. stands for independent and identically distributed .

r.v. denotes random variable

Law of Large Numbers (LLN)

According to the law, the average of the results obtained from performing the same experiment a large number of times should be close to the expectation value, and tend to be closer when n is even greater.

Let $X,X_1,X_2,\dots ,X_n$$X, X_{1}, X_{2}, \ldots, X_{n}$ be i.i.d. Laws (weak and strong) of large numbers (LLN):

Central Limit Theorem (CLT)

CLT establishes that when independent random variables summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed,

where $\stackrel{(d)}{\to }$$\stackrel{(d)}{\rightarrow}$ denotes convergence in distribution.

Standard Gaussian means that this quantity will be a number between (-3, 3) with overwhelming probability, we have $|{\bar{X}}_n-\mu |=\frac{3\sigma }{\sqrt{n}}$$\lvert \overline X_n - \mu\rvert =\frac{3\sigma}{\sqrt{n}}$.

${\overline{X}}_n$$\bar X_n$ is close to $\mu$$\mu$ at some deviations that are of order 1 over square root of sample size ($\sim \frac{1}{n}$$\sim \frac{1}{n}$).

Rule of thumb to apply CLT - normally, we require $n\ge 30$$n\geq30$.

Asymptotic normality

Assuming the sequence $\{X_n\}$$\{X_{n}\}$ is an i.i.d sequence with finite mean and variance. Therefore, it satisfies the conditions of Central Limit Theorem.

Hence, the sample mean ${\overline{X}}_n$$\bar X_{n}$ in the above equlity is asymptotically normal. In other words, the sample mean $X_n$$X_{n}$ converges in distribution to a normal random variable with mean $\mu$$\mu$ and variance $\frac{{\sigma }^2}{n}$$\large \frac{\sigma^{2}}{n}$.

Continuous Mapping Theorem (CMT)

CMT states that continuous functions preserve limits even if their arguments are sequences of random variables. A continuous function $f(\cdot )$$f(\cdot)$​ is such a function that maps convergent sequences into another convergent sequen,

It applies to $d,p$$d,\ p$ and $a.s.$$a.s.$ convergence respectively.

But how close is $f(T_n)$$f(T_n)$ to $f(T)$$f(T)$? The Delta ($\mathrm{\Delta }$$\Delta$) method.

Hoeffding's Inequality

What if $n$$n$ is not large enough to apply CLT?

For bounded random variable, this is still Hoeffding’s Inequality we can say for any n. Let $n$$n$ be a positive integer and $X_i\in [a,b]$$X_i \in[a, b]\ $($a<b$$a<b$ are given numbers) Then this holds even for small sample sizes $n$$n$:

Here I need that my random variables are actfually almost surely bounded, which rules out like Gaussians and Exponential Random Variables.

How to choose $\epsilon$$\varepsilon$ ?

So let's parse this for a second… , if when $\epsilon =\frac{c}{\sqrt{n}}$$\varepsilon = \large\frac{c}{\sqrt{n}}$:

The square root of $n$$n$ qualitative behavior happens at any n.

So the conclusion is the average is a good replacement

Is this tight? That's the annoying thing about inequalities.

The above inequality could actually be e to the minus exponential of n ($e^{-n}$$e^{-n}$), which could be much, much smaller than that, so it is loose.

Chebyshev Inequality & Markov Inequality

These two inequalities guarentees that upper bounds on $\mathbf{P}(X\ge t)$$\mathbf{P}(X \geq t)$ based on the mean and variance of $X$$X$.

Markov inequality

For a random variable $X\ge 0$$X \geq 0$ with mean $\mu >0$$\mu>0$, and any number $t>0$$t>0$ :

Note that the Markov inequality is restricted to non-negative random variables.

Chebyshev inequality

For a random variable $X$$X$ with (finite) mean $\mu$$\mu$ and variance ${\sigma }^2$$\sigma^{2}$, and for any number $t>0$$t>0$,

Remark: When Markov inequality is applied to $(X-\mu {)}^2$$(X-\mu)^{2}$, we obtain Chebyshev's inequality. Markov inequality is also used in the proof of Hoeffding's inequality.

Triangle Inequality

Slutsky’s Theorem

Slutsky's Theorem will be our main tool for convergence in distribution.

Let $T_n,U_n$$T_{n},U_{n}$​ be two sequences of r.v., such that:

Then,

• $T_n+U_n\stackrel{(d)}{\underset{n\to \mathrm{\infty }}{⟶}}T+U$$T_{n}+U_{n} \stackrel{(d)}{\underset{n \rightarrow \infty}{\longrightarrow}} T+U$,

• $T_n{U}_n\stackrel{(d)}{\underset{n\to \mathrm{\infty }}{⟶}}TU$$T_{n} U_{n} \stackrel{(d)}{\underset{n \rightarrow \infty}{\longrightarrow}} T U$

• If in addition, $u\ne 0$$u \neq 0$, then $\frac{T_n}{U_n}\stackrel{(d)}{\underset{n\to \mathrm{\infty }}{⟶}}\frac{T}{U}$$\large \frac{T_{n}}{U_{n}} \stackrel{(d)}{\underset{n \rightarrow \infty}{\longrightarrow}} \frac{T}{U}$.

Delta ($\mathrm{\Delta }$$\Delta$) method

https://en.wikipedia.org/wiki/Delta_method

Distribution

Discrete: Probability mass function

• Bernoulli, Uniform, Binomial, Geometric

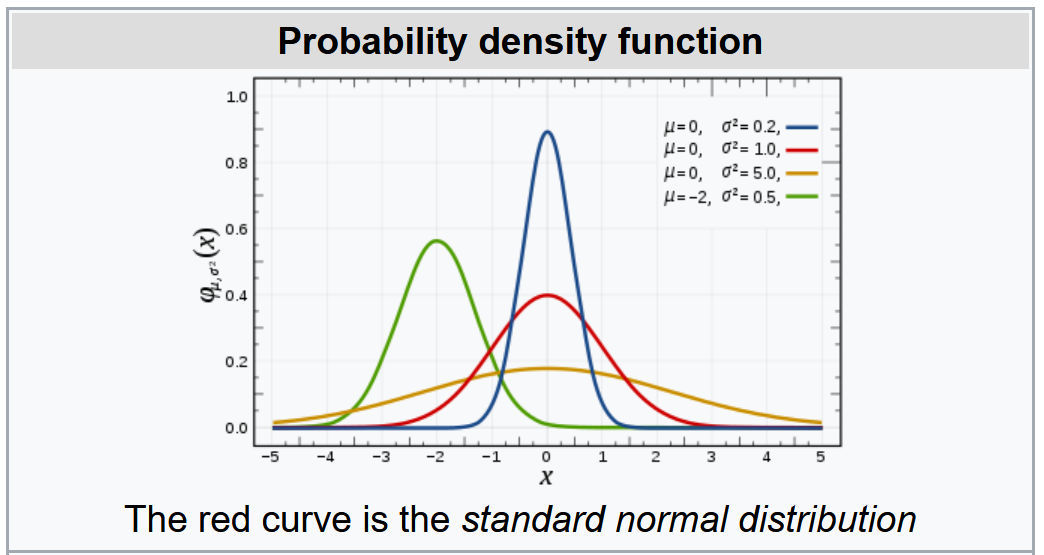
Gaussian Distribution

Notation: $X\sim \mathcal{N}(\mu ,{\sigma }^2)$$X\sim\mathcal{N}(\mu, \sigma^2)$

Mean and Variance: $\mu ,{\sigma }^2$$\mu,\ \sigma^2$

Probability Density Function:

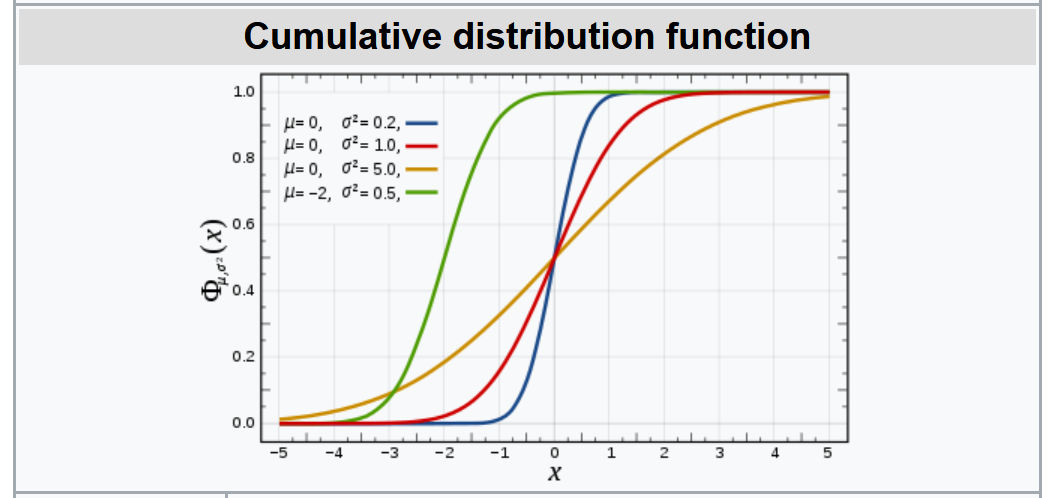
Cumulative Distribution Function:

$\text{erf}(\cdot )$$\text{erf}(\cdot)$ is the exponential response formula.

Why we use Gaussian Distribution so frequently?

Normally, we use sample mean as our estimator. And the reason is because the Gaussian distribution is the thing that shows up as the limit of the CLT as the minute you start talking about averages.

Of the universe type of results, that says that if you take average of enough things, then it's going to go to a Gaussian.

The extreme value?

The value field of a Gaussian is $(-\mathrm{\infty },\mathrm{\infty })$$(-\infty, \infty)$, but when we use it in mapping real distribution, namely the height, we will never achieve negative value, why we do Gaussian?

Yes, there exists extreme value, but they never really come into play. Because of the exponential can get really, really small. The Gaussian actually almost in a bounded interval.

Gaussian Probability Tables

A Gaussian CDF (z-score) calculator.

Quantiles

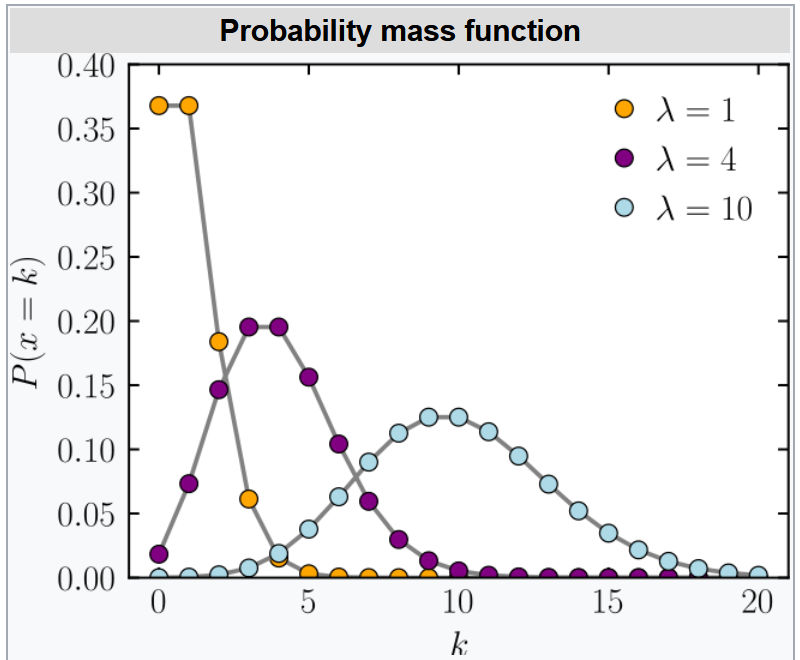
Poisson Distribution

The advantage of using poisson distribution is that n or p do not need to be known! This can make assumptions much easier.

Notation: $X\sim \text{Poi}(\lambda ),\lambda \in (0,\mathrm{\infty })$$X\sim\text{Poi}(\lambda),\ \lambda \in (0, \infty)$

Mean and Variance: $\lambda ,\lambda$$\lambda,\ \lambda$:

Pre-require 0! = 1

Probability Mass Function:

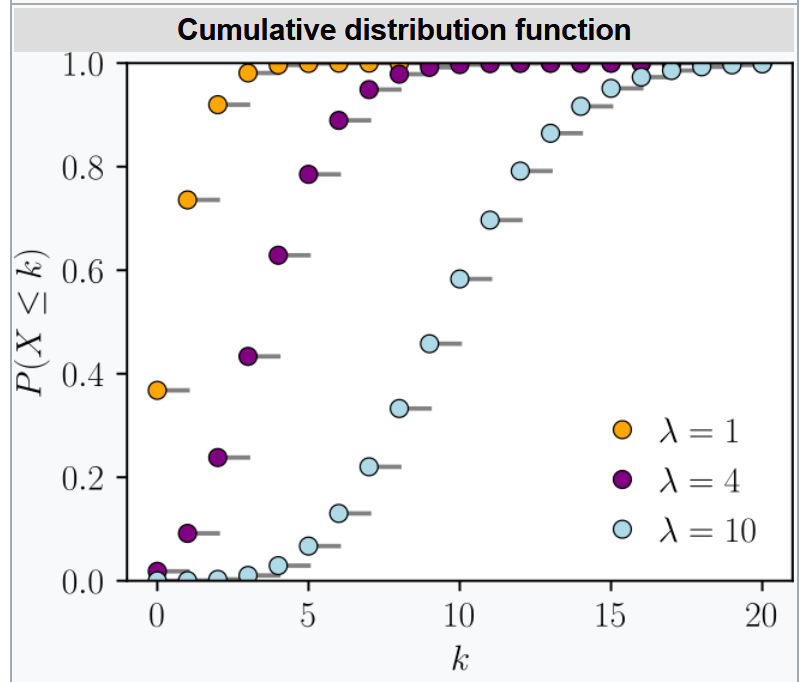
Cumulative distribution function:

Exponential Distribution

sample space: $x\in [0,\mathrm{\infty })$$x\in [0, \infty)$

Mean and Variance: $\frac{1}{\lambda },\frac{1}{{\lambda }^2}$$\large \frac{1}{\lambda},\frac{1}{\lambda^2}$

Probability Mass Function:

Cumulative distribution function:

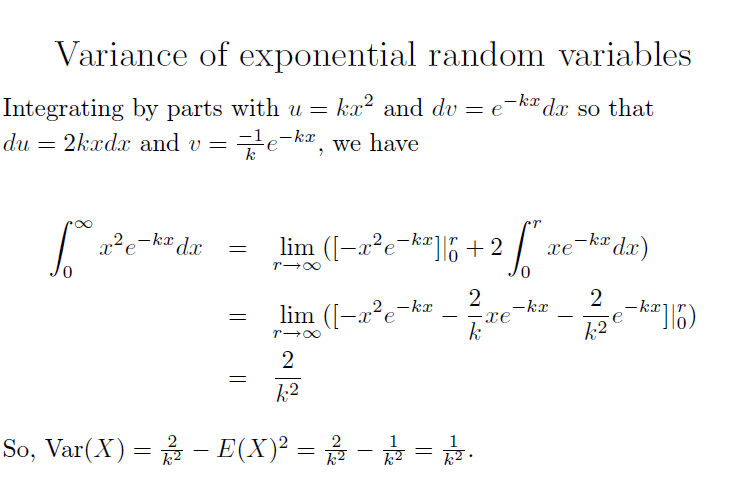
Gamma Distribution

Notation: $X\sim \text{Gamma}(\alpha ,\beta )\text{ or }\mathrm{\Gamma }(\alpha ,\lambda ),\lambda =\frac{1}{\beta }$$X\sim\text{Gamma}(\alpha,\beta)\text{ or } \Gamma(\alpha, \lambda) ,\lambda = \large \frac{1}{\beta}$

Parameters: $\alpha ,\lambda \in (0,\mathrm{\infty })$$\alpha, \lambda \in (0,\infty)$

Mean and Variance: $\frac{\alpha }{\lambda },\frac{\alpha }{{\lambda }^2}$$\large \frac{\alpha}{\lambda},\ \frac{\alpha}{\lambda^2}$

Gamma Function:

Probability Mass Function:

Cumulative distribution function:

Geometric Distribution

Such as : number of trials until a success

Geometric Distribution is either one of below two distribution:

• The probability distribution of the number $X$$X$ of Bernoulli trials needed to get one success, supported on the set $\{1,2,3,\dots \}$$\{1,2,3, \ldots\}$;

• The probability distribution of the number $Y=X-1$$Y=X-1$ of failures before the first success, supported on the set $\{0,1,2,\dots \}$$\{0,1,2, \ldots\}$.

Notation: $X\sim \text{Gemo}(p)\text{ or }Y\sim \text{Gemo}(p)$$X\sim\text{Gemo}(p)\ \text{ or }\ Y\sim\text{Gemo}(p)$

Mean and Variance: $\frac{1}{p}\text{ or }\frac{1-p}{p},\frac{1-p}{p^2}$$\large \frac{1}{p} \small\text{ or }\large \frac{1-p}{p} ,\ \frac{1-p}{p^2}$

Probability Mass Function:

Cumulative distribution function:

Binomial Distribution

Notation: $B(n,p)$$B(n,p)$, n is number of trials and p is success probability of each trial

Mean and Variance: $np$$np$, $\sum _{k=1}^n{\sigma }^2=np(1-p)$$\sum^n_{k=1} \sigma^2 = np(1-p)$

Probability Mass Function:

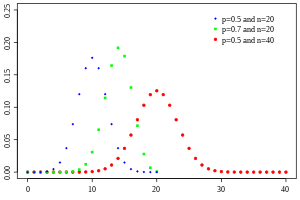
Cumulative Distribution Function:

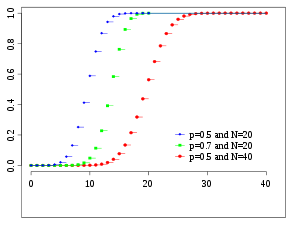
In other words, there are a finite amount of events in a binomial distribution, but an infinite number in a normal distribution.

Bernoulli Distribution

Notation: $X\sim Ber(p)$$X\sim Ber(p)$

Mean and Variance: $p$$p$, $p(1-p)$$p(1-p)$

PMF pmfs

Indicator Function

The indicator function of a subset $A$$A$ of a set $X$$X$ is a function

defined as

Derivative of indicator function

I have an indicator function $I(D\le Q)$$I(D\leq Q)$,

δ is symmetric. δ can be thought of as the derivative of the Heaviside function H(x)=1 for x>0, 0 for x<0.

Moment Generation Function (MGF)

https://en.wikipedia.org/wiki/Moment-generating_function

expectation of moment generating function

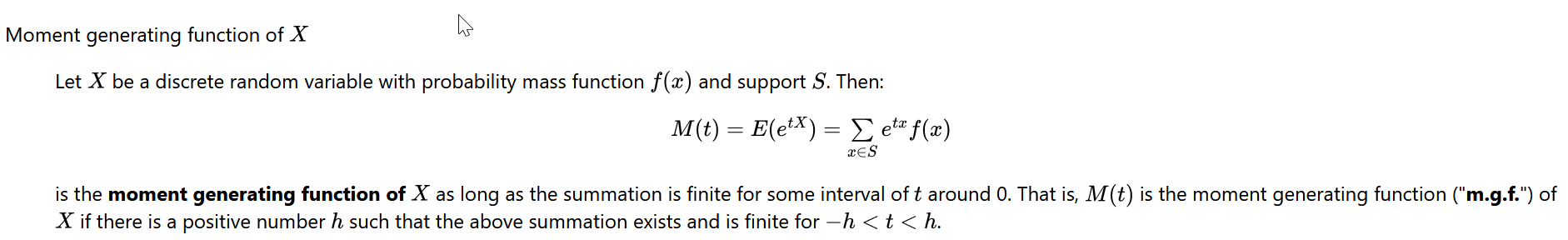
https://online.stat.psu.edu/stat414/book/export/html/676

mixture distribution moment generating function

Useful…

https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwitz--mtvL1AhXeQEEAHSmoAI8QFnoECDwQAQ&url=https%3A%2F%2Fwww.le.ac.uk%2Fusers%2Fdsgp1%2FCOURSES%2FMATHSTAT%2F6normgf.pdf&usg=AOvVaw3QHSFjpCFrBgTFBxRwGAnK---

Property of Distribution

We take Gaussian $X\sim \mathcal{N}(\mu ,{\sigma }^2)$$X\sim\mathcal N(\mu, \sigma^2)$as an example.

Affine Transformation:

Standardization:

According to CLT, we assume $Z=\frac{X-\mu }{\sigma }$$Z = \frac{X-\mu}{\sigma}$,

Symmetry:

Mode of Convergence

Three types of convergence, going from strong to weak.

• ${\left(T_n\right)}_{n\ge 1}$$\left(T_{n}\right)_{n \geq 1}$ is a sequence of random variables

• $T$$T$ is a random variable ( $T$$T$ may be deterministic).

• Some examples are shown [here]

Almost surely (a.s.) convergence

So I created two sequences, and I want this to converge.

Convergence in probability

The probability that they depart from each other by something is going to be going to 0 as $n$$n$ goes to infinity.

Convergence in distribution

This just saying I'm going to measure something about this random variable, maybe it is distribution. For all continuous and bounded function $f$$f$, using CLT:

I'm just saying that its distribution is converging. My random variable is going to become the same as the probabilities for the second guy as $n$$n$ goes to infinity.

Properties

• If ${\left(T_n\right)}_{n\ge 1}$$\left(T_{n}\right)_{n \geq 1}$ converges a.s., then it also converges in probability, and the two limits are equal a.s.

• If ${\left(T_n\right)}_{n\ge 1}$$\left(T_{n}\right)_{n \geq 1}$ converges in probability, then it also converges in distribution

Convergence in distribution implies convergence of probabilities if the limit has a density (e.g. Gaussian):

Addition, Multiplication and Division Assume,

Then,

• $T_n+U_n\stackrel{\text{ a.s./P }}{\underset{n\to \mathrm{\infty }}{⟶}}T+U$$T_{n}+U_{n} \stackrel{\text { a.s./P }}{\underset{n \rightarrow \infty}{\longrightarrow}} T+U$,

• $T_n{U}_n\stackrel{\text{ a.s. }/\mathrm{P}}{\underset{n\to \mathrm{\infty }}{⟶}}TU$$T_{n} U_{n} \stackrel{\text { a.s. } / \mathrm{P}}{\underset{n \rightarrow \infty}{\longrightarrow}} T U$,

• If in addition, $U\ne 0$$U \neq 0$ a.s., then $\frac{T_n}{U_n}\stackrel{\text{ a.s. }/\mathbf{P}}{⟶}\frac{T}{U\to \mathrm{\infty }}$$\large\frac{T_{n}}{U_{n}} \stackrel{\text { a.s. } / \mathbf{P}}{\longrightarrow} \frac{T}{U \rightarrow \infty}$.

Warning: In general, these rules do not apply to convergence in distribution $(d)$$(d)$.

Estimator

Normally, we have two estimator:

• Compute the expectation of your random variable

• Using Delta method

How can we decide how many samples ($n$$n$) we need to draw our conclusion? What is the cutoff, namely if 60 is enough, how about 59 and 58?

Now we have our first estimator of $p$$p$ of Kissing Example, we put a hat on everything that’s the estimator of something.

• For $i=1,\dots ,n$$i=1, \ldots, n$, define $R\sim Ber(p)$$R\sim Ber(p)$, $R_i=1$$R_{i}= 1$ if the $i$$i$ th couple turns to the right RIGHT, $R_i=0$$R_{i}=0$ otherwise.

• Our first estimator of $p$$p$ is the sample averge:

And averages of random variables are essentially controlled by two major tools: They are LLN and CLT.

What is the accuracy of this estimator?

What is the probability that $\hat{p}$$\hat p$ is away from $p$$p$ by more than 10%.

We don’t even know the trueandard and the observation $\hat{p}$$\hat{p}$ is from random variables fluctuates. We need a method to measure its fluctuation.

Modelling Assumptions:

• Each r.v. and i.i.d $R_i$$R_i$ is Bernoulli (p)

•  

Measures of Distance

If we want to estimate mean of a Gaussian and we can compute the expectation, but not it doesn’t work for the the variance.

You can go into example and compute the variance, which is actually coming from the method of moments.

But it turns our we have a much more powerful method called the maximum likelihood method, but it is far non-trivial.