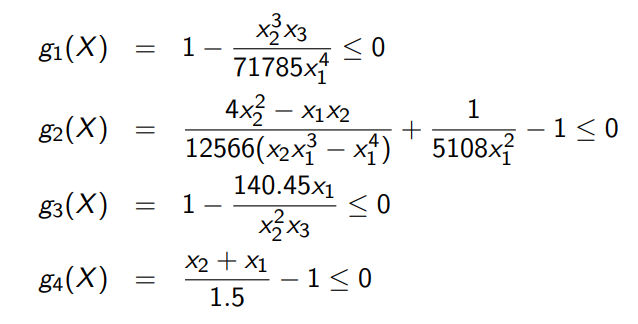“The study of computational systems that use ideas inspired from natural evolution, e.g., the principle of survival of the fittest.”
Evolutionary Computation
EC provides a general method for solving ‘search for solutions’ type of problems, such as optimisation, learning, and design.
Progress:
Week 2…
What will be covered?
Algorithms
Evolutionary Algorithms: Genetic Algorithms, Genetic Programming, Evolutionary Programming, Differential Evolution and Evolution Strategies
Game Theory (optimisation) and Evolutionary Game Theory (dynamics)
Particle Swarm Optimiser & Ant Colony Optimisation
Artificial Immune System
Theory
Schema Theorem -
Convergence and Convergence Rate -
Computational Complexity -
No Free Lunch Theorem
Fitness Landscape
Boolean Networks
Cellular Automata (including Game of Life)
Categories of Algorithms by by design paradigm
Divide and conquer algorithms, e.g., quicksort algorithm
Dynamic programming algorithms
Mathematical programming algorithms, e.g., linear programming
Search and enumeration algorithms
Brute force (exhaustive) algorithms, enumerating all possible candidate solutions and check
Improved brute force algorithms, e.g., branch and bound algorithms
Heuristic algorithms
Local search, e.g., greedy search
Randomised algorithms, which include Evolutionary Computation, etc
###
Travelling salesman problem (TSP)
Given a list of cities
Seek for the shortest rout that visits each city exactly once and returns to the origin city.
Solve TSP using:
Brute force
Mathematical programming algo, e.g. linear programming (itself is a NP-hard problem, see here).
So Heuristic algotithms
Randomised Algorithm
Start with Question: Matching one Bolt to n Distinct Sizes Nuts:
given one bolt and a collection of n nuts of different sizes, find a nut match the bolt
The brute-force solution time complexity: O(n2)
Answer: For many problems, a randomised algorithm is the simplest, the fastest.
Heuristic Algo
CS definition of heuristic: a (usually simple) algorithm that produces a good enough solution for a problem in a reasonable time frame
heuristic: find or discover non-optimal but satisfactory
Trad of optimality, completness, accuracy or precision for speed.
Includes determiistic (e.g. 0 or 1 results)
makes random choices during execution,
output and runtime can vary even with fixed input.
Use random number to help find and improve the solutions.
Two representatives:
Las Vegas Algo
may result in infinite loop until the correct solution
xxxxxxxxxxRepeat:Random search 1 element out of n samples.until a == xendthe worst runtime complexity is unbound
Monte Carlo Algo (蒙特卡罗)
runs for a fixed number of steps
xxxxxxxxxxi = 0Repeat:Random search 1 element out of n samples.i += 1;until (a == x) || (i == k)end
O(1) is fixed
Randomised Quicksort Algo
avg: O(nlogn), worst: O(2nlogn)

Local Search Algorithms
A heuristic algorithm for solving hard optimization problems.
Idea: start with an initial guess at a solution and incrementally improve it until it is one
Incremental improvement: local changes, e.g., the algorithm iteratively moves to a neighbour solution
Neighbour solution: Depends on the definition of a neighbourhood relation on the search space, but generally based on similarity (distance) measure
Hill Climbing Algo
Climbing Everest in thick fog with amnesia
Search for its better Immediate neighbour solutions, which is the most similar solutions to the current solution.
Two types of hill climbing:
Simple hill climbing: chooses the first better solution
Steepest ascent hill climbing: compares all neighbour solutions and chooses the best solution
2-Opt Algorithm
Detailed swapping steps for swapping two edges, which result in an immediate neighbour solutions:
Step 1: removal of two edges from the current route, which results in two parts of the route.
Step 2: reconnect by two other edges to obtain a new solution
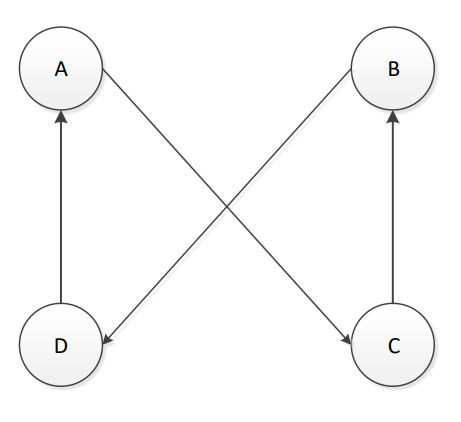
What is 3-Opt Algo?
#TODO How to draw fitness landscape in high dimension?
Randomised search vs Local search
Random
Good at exploration, Not good at exploitation
Especially bad for problems solution only lies on narrow space.
Local
Not good at exploration: gets stuck in local minima.
Good at exploitation: capable of finding local optimum
Stochastic Local Search algorithms
Main idea: escape or avoid local optima, introduce randomness into local search algo.
Escape stategies:
Random restart: simply restart the local search from a random initial solution
Perform non-improving step: randomly move to a less fit neighbour – Simulated Annealing (SA)


Accepting worse solutions with a certain probability, e.g.,
Other: Tabu Search
Evolutionary Algorithms

An Evolutionary Algorithms consists of: representation: each solution is called an individual fitness (objective) function: to evaluate solutions variation operators: mutation and crossover selection and reproduction : survival of the fittest



Genetic Algorithm (GA)
natrual selection: survival of the fittest,
Observation: Natural Evolution has evolved many complex systems (e.g., brain) and ”solved” many bioengineering problem.
Driving Force: Simulate Genetic variations that enhance survival and reproduction become and remain more common in successive generations of a population (idea of Darwinian Evolution).
Initialization: requires many setting, including initial population, population size, selection, reproduction, mutation, and criteria for termination of algorithm.
Genotype (基因型): Binarye encoded solution
Phenotype (表现型): Decode solution from Genotype.
Genetic variation Operators
Mutations: changes in the DNA (Deoxyribonucleic Acid) sequence.
Flip each bit with a probability
Together with selection what mutation actually does is stochastic local search: it exploit current good solutions by randomly explore near search space
Crossover: reshuffling of genes through sexual reproduction and migration between populations
Randomly select two parents with probability
K-point crossover: Select
Uniform crossover: For each
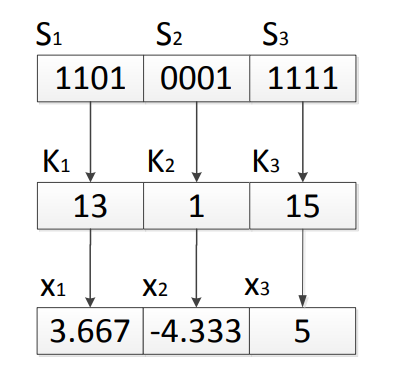
Decoding Function
We have
Divide
Decode each
Apply decoding function
For example, assume
Selection
Selection usually is performed before variation operators: selects better fit individuals for breeding
Emphasising on exploiting better solutions in a population:
Select one or more copies of good solutions.
Inferior solutions will be selected but with a much less chance
Question: Why we still select those inferior solutions?
Allows some weak individuals who may help escaping from local optima. Because super individuals normally cause low separation among individuals, lead to premature convergence to a local optimum.
Selection schemes:
Fitness Proportional Selection
Selecting individual
where
Don’t allow negative value.
High fitness individual will still have chances to get elimated.
low fitness individual can survive the selection, to add more separation.
How to maintain selection pressure throughout the run?
Linear Scaling:
usually we set
Ranking Selection
Select top
linear ranking
Assume
i.e. best individual
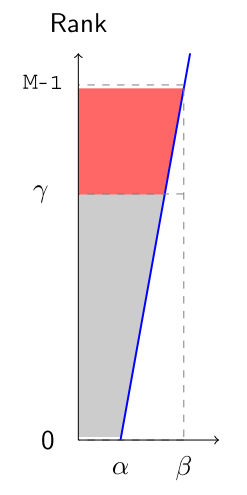
How to set
exponential ranking
power ranking
geometric ranking
Truncate selection
Step 1: Rank individuals by fitness values
Step 2: Select some proportion
Tournament Selection
Binary tournament selection (
Step 1: Randomly sample a subset
Step 2: Select the individual in
Repeat Steps 1 and 2 until enough offspring are created
Parent population of size
Generate
Next population is
Pros and Cons of GA
Selection pressure is the degree to which selection emphasises on the better individuals.
Scheme is a template that identifies a subset of strings with similarities at certain string positions
Pros:
Binary GA maximises the level of implicit parallelism.
Implicit parallelism:
we are not only evolving

Drawbacks of Binary Coding
Problem in discrete search spaces
Redundancy problem
when the variables belongs to a finite discrete set with a cardinal different from a power of two, some binary strings are redundant, which correspond infeasible solutions
Example: Suppose we have a combinatorial optimisation problem whose feasible set
Problem in continuous search spaces
Precision of Decoding depending on
Hamming cliff problem: one-bit mutation can make a large (or a small) jump; a multi-bit mutation can make a small (or large) jump.

Solution - Gray encoding
For

Mutation
randomly select a parent with
Uniform Mutation
replace
Non-uniform Mutation
replace
Gaussian Mutation
replace
typically, the
Crossover
Randomly select two parents
Flat crossover
offspring
Simple crossover
a cross value point
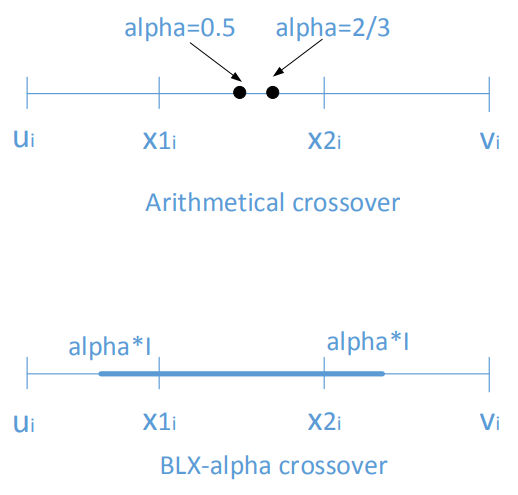
Whole arithmetical crossover
Single arithmetical crossover
choose a gene and then replace it with the arithmetic average of genes at the position of two parents, other genes are copied from the parents.
BLX-
GA Example Problem
A company is evaluating 4 projects which each run for 3 years and have the following characteristics.
Decision problem: Which projects should be selected to maximize the total profits?
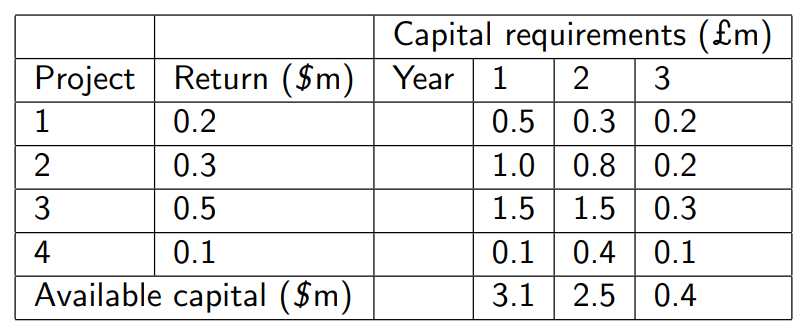
Once a project has been selected, all yearly capital requirement (investments) and capital (budget) must be met.

Constraint Handling in Evolutionary Algorithms
Below is a benchmark which can be used to test the constraint optimization algorithm:

So we want to minimize:
Subject to